中文
English

在探索微观世界的征程中，无论是观察还是“雕刻”，我们始终面临着一个根本性的物理限制——衍射极限。这个源于波的衍射天性的限制，如同一个无形的屏障，决定了我们能看清多小的物体，能加工多精细的结构。然而科学的魅力恰在于不断挑战并突破极限，本文将从物理直觉出发，深入浅出地探讨衍射极限的本质，比较光学与电子束在此限制下的表现，并最终延伸至激动人心的超分辨率技术。

衍射极限：看得见的“模糊”边界

想象一下，你试图用一个水波去探测水中的一根细柱子。如果柱子比波长宽得多，波浪会在柱子后方形成清晰的影子，你可以轻易判断柱子的存在和位置。但如果柱子变得非常细，甚至比水波的波长还要窄，那么波浪将不再形成清晰的影子，而是会“绕过”柱子继续传播，仿佛柱子不存在一样。这个现象就是衍射。

同样，光作为一种电磁波，在通过透镜（例如显微镜的物镜）汇聚成像时，也会发生衍射。一个理想的点光源，经过完美的光学系统后，并不会形成一个无限小的亮点，而是一个中心亮、周围环绕着明暗交替同心圆环的图案，这个图案被称为艾里斑。 这个光斑的大小，直接决定了光学系统的分辨能力。

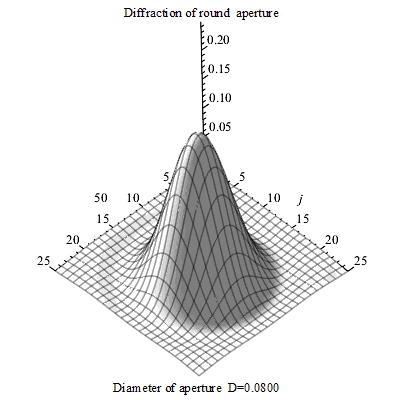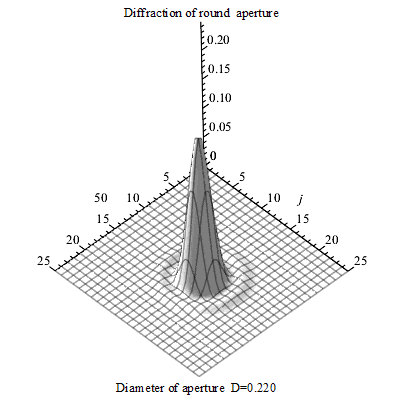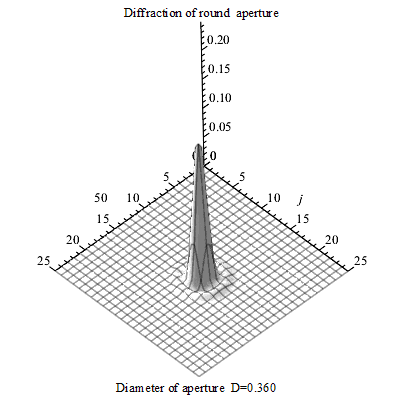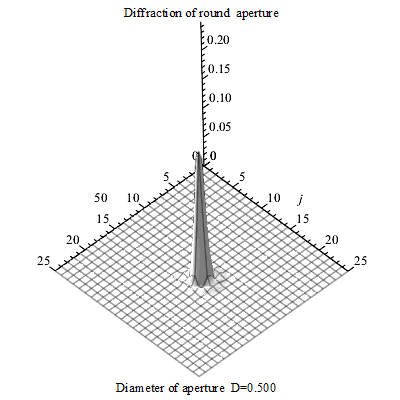
图 艾里斑随圆孔直径的变化3D图

物理直觉：你可以将透镜想象成一个光的“闸门”。光波通过这个有限大小的闸门时，其传播方向会发生一定程度的弥散，无法被完美地聚焦到一点。这个“闸门”开得越大（即数值孔径NA越大），或者通过的波的“个头”越小（即波长λ越短），衍射效应就越不明显，聚焦的光斑也就越小。

19世纪的物理学家恩斯特·阿贝（Ernst Abbe）将此规律量化，提出了阿贝衍射极限公式：

d=λ/(2n*sinθ)=λ/(2*NA)

其中：

d 是系统能分辨的两个点之间的最小距离，即分辨率。

λ 是所用波的波长。

n 是介质的折射率。

θ 是透镜收光锥角的半角。

NA=n*sinθ 是数值孔径，表征了透镜汇聚光线的能力。

这个公式直观地告诉我们，要想看得更清楚（d更小），只有两条路可走：要么缩短波长λ，要么增大数值孔径NA。 然而，对于传统光学显微镜，可见光的波长范围约为400-700纳米，而NA值受限于材料和物理尺寸，通常最大也就在1.4左右。这使得传统光学显微镜的分辨率极限被“锁死”在200纳米左右，对于更小的病毒、蛋白质分子或芯片上的纳米结构便无能为力。

图 电磁波谱·光谱

从光子到电子：一场分辨率的革命

既然光的波长限制了我们前进的脚步，科学家们便将目光投向了拥有更短波长的粒子——电子。根据路易·德布罗意于1924年提出的物质波理论，运动的粒子也具有波动性，其波长（德布罗意波长）λ 与其动量 p 成反比：

λ=h/p（h 为普朗克常数）

当电子被高电压加速时，其速度极快，动量极大，因而对应的波长可以变得非常短。例如，在一个加速电压为10千伏（kV）的电子显微镜中，电子的波长约为0.12埃（Å），即0.012纳米，这比可见光的波长短了数万倍！

这种波长上的巨大优势，使得电子束成为探索和加工纳米世界的理想工具。扫描电子显微镜（SEM）和透射电子显微镜（TEM）利用电子束作为“光源”，轻松地将分辨率提升至纳米甚至亚纳米级别，让我们得以窥见原子尺度的世界。

同样地，在微纳加工领域，电子束光刻（EBL） 技术也利用了电子束的短波长优势。它使用聚焦后的高能电子束，像一支超高精度的“笔”，直接在涂有感光材料（抗蚀剂）的基底上进行“绘制”，从而定义出极其精细的电路图案。